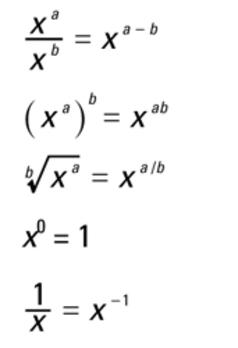(0rder of Operations)
Circle the terms Use P*E*M*D*A*S
1. Get each term(circle) to have only one number. i. Parenthesis
2. Get each term circle to have one number 2.Exponents
3. Change subtraction to addition.
4. Add ALL positive and negative 3.Multiply and Divide
5.Simplify
1. 15 + (-7) -6(2)=
2. 11 (-5) + (-3) x 2 =
3.5-5-(-5) + (-15) + 30 =
4. (3 - 10) + 16-6 • (-4) =
5. (-3)'4'(-2)-(-20)+12=
6. -7-(-5) + 3 • (-7) =
7. 10 x3 - (-8)'5 + (-5)-(12)=
8. (3 - 8) + 4 - (-1) x (-2) -9 =
9. -15+ 4-(5)-3'(4)=
10. 2 • [-6-(-6)] + (-5)-7
NUMBER LINE
-20 -19 -'18 -17 -I6 --15 -14 --13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
ABSOLUTE VALUE -(The distance a number is from zero)
How far away from zero is the number ? The result is always positive because the direction needed to go does not matter.
ABSOLUTE VALUE PROBLEMS
Directions: Write the result to the following expressions. Be careful to find the absolute value of the
correct numbers at the appropriate times.
1. I 9 I = 2. I -19 I = 3. I 59 I =
4.I -33 I = 5. I 21 I = 6. I -42 I =
7. I 5 I = 8. | 28+ (-19) - 9. | = 9.I 2 6 | + (-14) I =
10. | 43+(-51) = 11. | 14+ (-27) I = 12.I -7 | + (- 22) =
13. |(- 10)+ (-28) | = 14. | (-19) | + | 37 | = 15. I (- 30) + (- 4 ) =
16. What two numbers have an absolute value of 8?
Fill in the appropriate symbol ( < > = ) to make a true statement.
17. |11| O 3 18. 14 O (- 2 ) 19. |7 O l-17l 20. (-2) 0 |-7I